definition sinus cosinus – définition cosinus sinus tangente
Par définition le sinus le cosinus et la tangente de l’angle aigu de sommet du triangle rectangle sont : Created with Raphaël Il faut bien comprendre que les mots hypoténuse opposé et adjacent désignent les longueurs de l’hypoténuse du côté opposé ou du côté adjacent à l’angle concerné,
Triangle rectangle : trigonométrie
En mathématiques les fonctions trigonométriques permettent de relier les longueurs des côtés d’un triangle en fonction de la mesure des angles aux sommets Plus généralement ces fonctions sont importantes pour étudier les triangles et les polygones les cercles et modéliser des phénomènes périodiques Les trois fonctions trigonométriques les plus utilisées sont le sinus le cosinus et la tangente, Les relations entre les …
Chapitre 11 Fonctions sinus et cosinus
· Fichier PDF
Cosinus et Sinus, Rappels, Dans un triangle rectangle le cosinus est défini comme le rapport du coté adjacent par l’hypoténuse tandis que le sinus de cet angle est défini comme le rapport du coté opposé par l’hypoténuse, cos α =, coté adjacent, sinus α =, coté opposé,
Explorez davantage
| Calculer le sinus, le cosinus ou la tangente d’un angle d | fr,khanacademy,org |
| Cosinus — Wikipédia | fr,wikipedia,org |
| Trigonométrie/Relations trigonométriques — Wikiversité | fr,wikiversity,org |
| Exercices de trigonométrie de seconde – CMATH | www,cmath,fr |
| Sinus, cosinus & tangente – Toutcalculer,com | www,toutcalculer,com |
Recommandé pour vous en fonction de ce qui est populaire • Avis
Définition du cosinus et du sinus avec le cercle
La fonction cosinus est une fonction mathématique paire d’un angle Dans un triangle rectangle le cosinus d’un angle est le rapport de la longueur du côté adjacent par la longueur de l’ hypoténuse
Cosinus et Sinus
Fonctions sinus et cosinus
Définition du cosinus et du sinus avec le cercle trigonométrique Mathématiques Lycée Supérieur
FONCTIONS COSINUS ET SINUS
· Fichier PDF
Cosinus, sinus et tangente
definition sinus cosinus
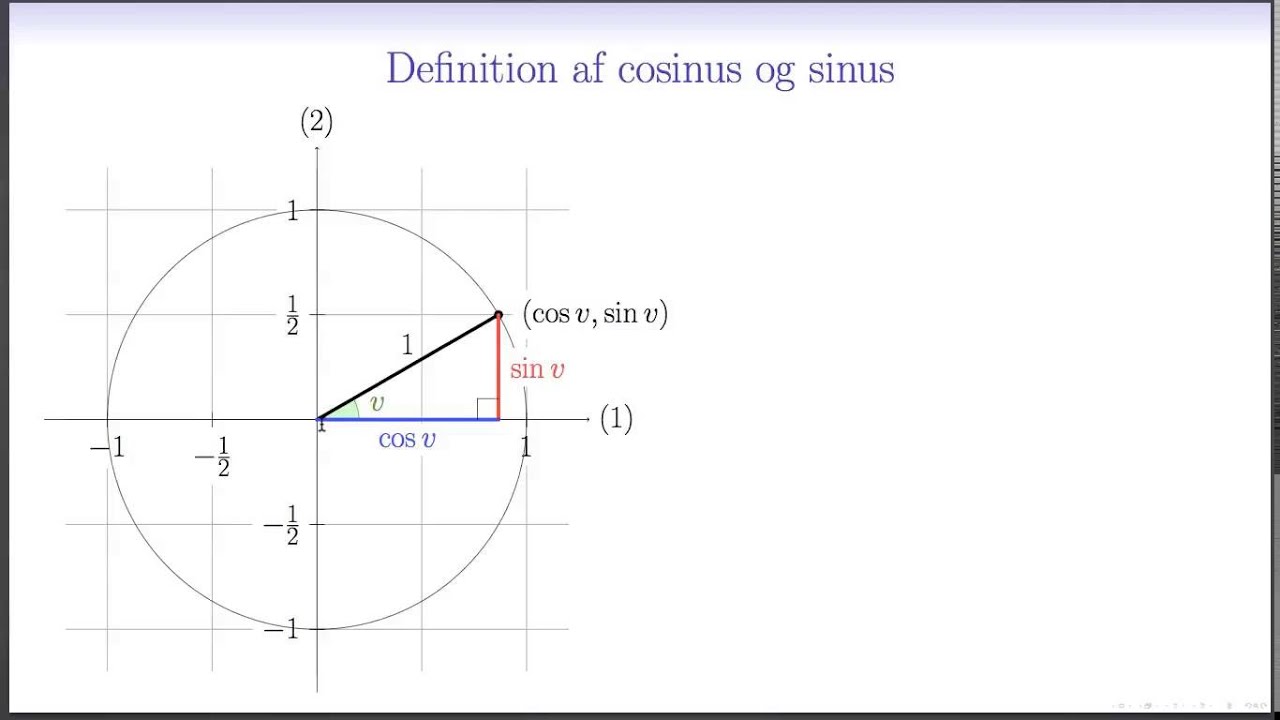
Définition 1 : Fonctions sinus et cosinus À tout réel x, on associe un point unique M du cercle unité de centre O, dont les coordonnées sont : Mcosx; sinx On définit alors les fonctions sin et cos sur R par : x 7→sinx et x 7→cosx sinx b cosx x M O 1,2 Mesure principale d’un angle
Tout savoir sur les fonctions trigonométriques sinus
· La fonction cosinus définie sur R et est une fonction paire: pour tout x ∈ R cos-x = cosx La courbe représentative de la fonction admet l’axe des ordonnées comme axe de symétrie comme on peut le constater sur le dessin ci-dessus La fonction cosinus est périodique de période 2π: pour tout x ∈ R cosx+2π = cos x On distingue en rouge dans le dessin ci-dessus une période de la fonction c’est-à-dire le plus …
Fonctions sinus et cosinus rappels et compléments I Rappels On rappelle ici les principaux résultats en trigonométrie établis dans les classes précédentes 1 Enroulement de l’axe réel sur le cercle trigonométrique Le plan est rapporté à un repère orthormé direct ŠO Ð→ I Ð→ J ‘ ou encore OXY Le cercle trigonométrique est le cercle de centre O et de rayon 1
Définition : sinus cosinus et tangente ABC est un triangle rectangle en B Le sinus de l’angle est le rapport des longueurs du côté opposé à cet angle et de l’hypoténuse, Le cosinus de l’angle est le rapport des longueurs du côté adjacent à cet angle et de l’hypoténuse,
Fonction trigonométrique — Wikipédia
Définitions : – Le cosinus du nombre réel x est l’abscisse de M et on note cos x – Le sinus du nombre réel x est l’ordonnée de M et on note sin x Propriétés : Pour tout nombre réel x on a : 1 −1≤cosx≤1 2 −1≤sinx≤1 3 cos2 x + sin2 x= 1 2 Valeurs remarquables des fonctions sinus et cosinus : x 0 π 6 π π 4 π 3 π 2 cosx 1 3 2 2 2
· Définitions Par le cercle trigonométrique niveau lycée Soit un point du cercle trigonométrique avec un angle x par rapport à l’axe des abscisses, Le cosinus est alors l’abscisse de ce point et le sinus en est l’ordonnée, Voici un schéma pour mieux comprendre,
Fonctions sinus et cosinus
· Fichier PDF
Définition : On dit qu’une fonction est périodique de période réel si elle est définie sur R et, pour tout réel on a , On sait que, du fait de la définition des sinus et cosinus d’un nombre, que, pour tout réel on a et , Par conséquent, les fonctions sinus et cosinus sont périodiques de période ,
Calculer le sinus le cosinus ou la tangente d’un angle d
La tangent se calcule dans un triangle rectangle en divisant le coté opposé à l’angle par le coté adjacent, Tangente = coté oposé, coté adjacent, Exemple: Tan  = CB, AC, Astuce mnémotechnique pour calculer un cosinus, un sinus ou une tangente, Il suffit de retenir la formule SOHCAHTOA qui, indique SOH : Sinus = Opposé : Hypothénuse,
Cosinus — Wikipédia
Bac de maths : Cosinus et Sinus