ellipse coordinates and equation – coordinate equation calculator

SeCtion 106 Conic Sections in Polar Coordinates 685 From Theorem 6 we see that this represents an ellipse with e−2 3,Since ed− 10 3 we have d− 10 3 e − 10 3 2 3 − 5 so the directrix has Cartesian equation x − 25 When −0 r −10; when − r −2 So the vertices have polar coordinates s10, 0d and s2, d,

ellipse coordinates and equation

Ellipse

The standard form of the equation of an ellipse with center 0,0 0, 0 and major axis parallel to the y -axis is, x2 b2 + y2 a2 =1 x 2 b 2 + y 2 a 2 = 1, where, a >b a > b, the length of the major axis is 2a 2 a, the coordinates of the vertices are 0,±a 0, ± a the length of the minor axis is 2b 2 b,

In the above common equation two assumptions have been made First that the origin of the x-y coordinates is at the center of the ellipse Second that the longer axis of the ellipse is along the x- axis The convention that the semi-major axis is the x-axis will be used throughout In this technical note both conventions for the coordinate system origin will be used The equations with the 2

Taille du fichier : 208KB

However, when you graph the ellipse using the parametric equations, simply allow t to range from 0 to 2π radians to find the x, y coordinates for each value of t, Other forms of the equation, Using the Pythagorean Theorem to find the points on the ellipse, we get the more common form of the equation, For more see General equation of an ellipse

Chapter Parametric Equations and Polar Coordinates

 · Fichier PDF

Equation of an Ellipse with Examples

29, It’s easiest to start with the equation for the ellipse in rectangular coordinates: x / a 2 + y / b 2 = 1, Then substitute x = r θ cos, ⁡, θ and y = r θ sin, ⁡, θ and solve for r θ, That will give you the equation …

Afficher plus de résultats

An ellipse is defined as the set of points that satisfies the equation In cartesian coordinates with the x-axis horizontal the ellipse equation is The ellipse may be seen to be a conic section a curve obtained by slicing a circular cone A slice perpendicular to the axis gives the special case of a circle For the description of an elliptic orbit it is convenient to express the orbital

Area of an Ellipse in Polar Coordinates—CE Mungan Fall 2017

 · Fichier PDF

Reduced Cartesian equation: , with principal semi-axes , When a = b or b = c: ellipsoid of revolution, or spheroid otherwise, the ellipsoid is said to be scalene, – when a = b: oblate ellipsoid of revolution shaped like a pebble or a flying saucer – when b = c: prolate ellipsoid of revolution shaped like a rugby ball or a cigar – when a = b = c: sphere,

Ellipses and Elliptic Orbits

 · Determine the equation for ellipses centered at the origin using vertices and foci, If we know the coordinates of the vertices and the foci, we can follow the following steps to find the equation of an ellipse centered at the origin: Step 1: We find the location of the major axis with respect to the x-axis or the y-axis, 1,1,

Ellipse Graph and Equation – GeoGebra

You are going to explore the equation of ellipse with center at There are four values you can change and explore Center coordinate Center in this app is written as You can change the value of h and k by dragging the point in the grey sliders The length of the horizontal segment from the center of the ellipse to a point in the ellipse You can adjust the length using the red slider, This

Ellipse Graph Explained with Equations and Solved Examples

 · The equations help us to draw an ellipse on a graph with the x & y coordinate planes This article will demonstrate how we can graph an ellipse from a given equation both in standard and general form To graph an ellipse we first need to find out its center foci vertices and co-vertices, The equations help us to find these parameters, From our ellipse article, we know that ellipses have 2

Standard equation, The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and: , the foci are the points = ,, = ,, the vertices are = ,, = ,,, For an arbitrary point , the distance to the focus , is + and to the other focus + +,Hence the point , is on the ellipse whenever:

Equations of Ellipses

Ellipsoid

Area of an Ellipse in Polar Coordinates—C,E Mungan Fall 2017 Consider an ellipse centered on the origin and with the x and y axes aligned along the semi- major axis a and the semi-minor axis b respectively, so that the equation of the ellipse in rectangular coordinates is x a ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 + y b ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 =1, 1 Convert to polar coordinates by substituting

trigonometry

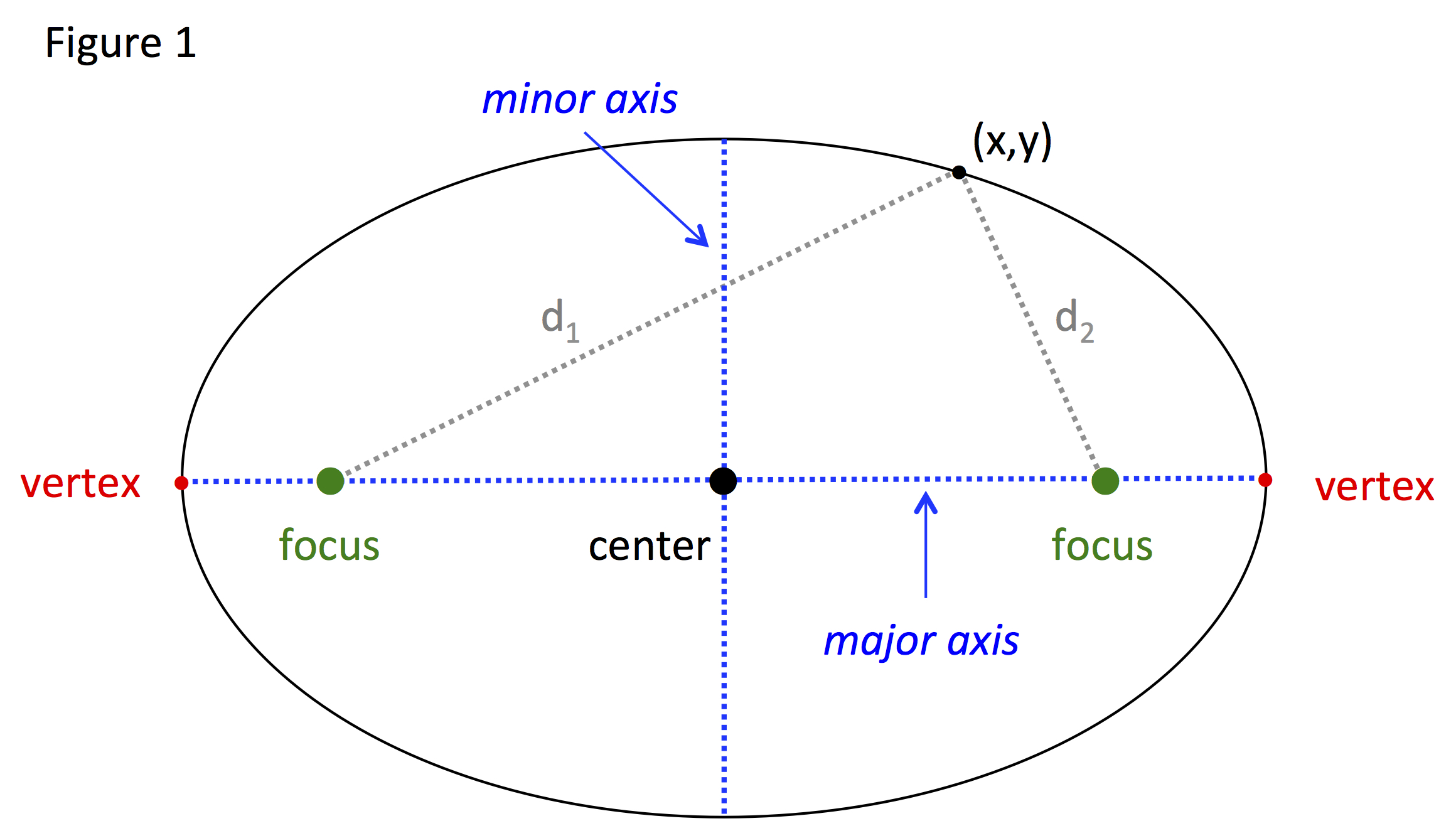
Equations of an Ellipse

 · Fichier PDF

Equation of an Ellipse with Center at the Origin

Parametric Equation of an Ellipse

Writing the equation for ellipses with center at the origin using vertices and foci, To find the equation of an ellipse centered on the origin given the coordinates of the vertices and the foci, we can follow the following steps: Step 1: Determine if the major axis is located on the x axis or on the y axis, 1,1, If the coordinates of the vertices have the form and the coordinates of the foci